Processing で目で見る画像処理 - フィルタ
画像処理なんだから目で見るのはあたりめーだろ、というツッコミは心の中にしまい込みましょう。
本投稿はProcessing Advent Calendar 2013の22日目の記事です。
無理やりねじ込んでいただきましてその節はありがとうございました。
のこり3日、完走まであと一息ですね!
次のような作品を作りました。ぽちぽちクリックorドラッグしてみてください。
どうにも最初の描画がうまくいかんのですが...
https://www.openprocessing.org/sketch/125994
解説
というより備忘録。
作品について
右の各ボタンをクリックすると、ボタンに応じたフィルタ処理が施され、処理後のLennaさん画像が表示されます。Lennaさんの画像をクリック(orドラッグ)すると、x座標を横軸に取ったRGBそれぞれの色値のグラフが下部に表示されます。
画像処理を施したときの画像の変化と画素値の変化をビジュアルでわかりやすくするための作品です。
ボタンの種類は以下。
| 画像 | 種別 | 画像 | 種別 |
|---|---|---|---|
 |
元画像 |  |
エッジ抽出 |
 |
先鋭化 | 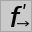 |
x軸微分 |
 |
平滑化 |  |
y軸微分 |
デジタル画像処理についてざっくりと
デジタル画像はx軸とy軸の空間における、RGBそれぞれの色値、アルファなどの多次元の信号から成る情報の集合です。
例えばこんな画像があったとして、

あるy座標に一本線を引きます。

上記の線分における色値の変化を、横軸:x座標、縦軸:色値でプロットすると

こんな感じになります。
y座標を変えると、


こんな感じです。
画像をこのような波形に捉えると、周波数だのフーリエ変換だのといった信号処理の概念を応用できるようになるんですねー。
フィルタ処理についてざっくりと
で、デジタル信号処理には「フィルタ」という概念がありまして、特定の周波数成分を抽出したり、ノイズをカットしたり、という目的に利用されます。
画像処理におけるフィルタは次のような3x3(または5x5など)の配列で表現されます。
| 0 | 1 | 0 |
| 1 | -4 | 1 |
| 0 | 1 | 0 |
このフィルタが意味するところは、対象の(x,y)座標のピクセルに対して、その周囲8ピクセルの重み付けを考慮して計算しましょう、というものです。
上の例だと、
after_C(x,y) = before_C(x-1, y-1) * 0 + before_C(x, y-1) * 1 + before_C(x+1, y-1) * 0 + before_C(x-1, y) * 1 + before_C(x, y) * -4 + before_C(x+1, y) * 1 + before_C(x-1, y+1) * 0 + before_C(x, y-1) * 1 + before_C(x+1, y+1) * 0 # before_C(x,y): フィルタ処理前の(x,y)座標のピクセルの色 # after_C(x,y): フィルタ処理後の(x,y)座標のピクセルの色
で、(x,y)座標のピクセルの色を計算することができます。
各種フィルタについてざっくりと
以下では作品で利用した各フィルタについてぼちぼち書きます。
 平滑化フィルタ
平滑化フィルタ
以下が平滑化フィルタの正体です。
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
計算式を書いてみるとわかりやすいですが、近傍の画素との平均を取って処理後の画素値とするフィルタです。
一般にノイズ除去に利用されるようです。特に、ごましおノイズと言われる、急激に高い(または低い)色値が紛れるようなノイズに有効です。あまりやりすぎるとピントがぼけたような画像になります。
| 平滑化前 | 平滑化後 |
 |
 |
グラフを見ても、このようにゆるやかな曲線に変化するのがわかりますね。
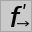
 微分フィルタ
微分フィルタ
学校で微分を習うのって高校でしたっけ?微分は「変化の割合」を表す、と習ったのではないかと思います。あるいは「接線の傾き」ですかね。以下が微分フィルタです。
x方向
| 0 | 0 | 0 |
| 0 | -1 | 1 |
| 0 | 0 | 0 |
y方向
| 0 | 0 | 0 |
| 0 | -1 | 0 |
| 0 | 1 | 0 |
上記を見てもらえばわかるように、お隣との差分を取る、という単純なフィルタです。
正方向への変化が急激であればあるほど、正方向に値が大きくなり、負方向への変化が急激であればあるほど、負方向に値が大きくなります。
| 微分前 | 微分後 |
 |
 |
 |
 |
つまり微分した画像とは、色の変化が急激なところが強調(抽出)された画像、ということになります。
画像(色)における急激な変化とは、すなわち「色と色との境界」にあたります。
そんなわけで、微分フィルタはエッジを抽出するフィルタとなります。
高校時代は面白くなかった微分も、こうして活用例がわかると面白くなってきますね!
 ラプラシアンフィルタ
ラプラシアンフィルタ
このボタンで適用されるのはラプラシアンフィルタと呼ばれるものでした。
ラプラシアンとは2次微分のことです。
フィルタは以下のようになりますが、導出については割愛します。
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
微分が「変化の割合」を表すので、2次微分は「変化の割合の変化の割合」を表します。こんがらがってきますね。
| 元画像 |
 |
| 1次微分 |
 |
| 2次微分 |
 |
ただし、上記のラプラシアンフィルタの場合は正負が反転して次のようになります。
| 上記のラプラシアンフィルタ |
 |
元画像の変化が始まるところと終わるところが抽出できるというのがわかります。
このとき正から負へ、または負から正へと変化する0交差点を検出すると、境界(エッジ)を得ることができます。(が、上の作品ではそこまでやってません。)
 先鋭化フィルタ
先鋭化フィルタ
先鋭化フィルタは以下のようなやつです。
| 0 | -1 | 0 |
| -1 | 5 | -1 |
| 0 | -1 | 0 |
フィルタの重みを見ていただくとわかるかと思いますが、ラプラシアンに元の画素値を足したものが処理結果となります。
ラプラシアンの結果が上で見たようになるので、これに元の値を足しこむと、
 |
+ |  |
| = |  |
このように変化が始まるところと終わるところ、すなわちエッジが強調された信号が得られます。
(わかりやすいように、少しスケールを変えてあります。)
境界が際立つことで、画像が先鋭化されるというわけですね。
先鋭化フィルタについて学んだときには感動しました。
いや、先鋭化された画像もスゲーなあと思いましたが、何よりその計算の仕組みにえらく感心した覚えがあります。
まとめ
以上が画像処理、主にフィルタについてでした。
実例を伴って学ぶ楽しさが実感できると、勉強も苦ではなくなりますよね。
こういったやりたいこと、試したいことを簡単にインタラクティブ性を持たせて実現できるProcessingはかわいいやつですね!
そんなこんなで日々精進したいと思います。(適当)